[9]:

import quanguru as qg
import numpy as np
import matplotlib.pyplot as plt

14 - Time dependent Hamiltonian#

In previous tutorials, the system Hamiltonians were time independent, and QuanGuru provides couple different methods to describe and simulate time-dependent Hamiltonians. In this tutorial, we demonstrate one (probably the most convenient and flexible) of these time-dependent Hamiltonian methods.

Here, we use the below single qubit Hamiltonian,

H=f_{z}J_{z} + f_{x}(t)\sigma_{x}

where the second term will be time dependent.

[10]:

qubFreq = 1
driveFreq = 2
driveAmp = 1
drivePhase = 0
couplingStrength = 1

OmegaR = couplingStrength*driveAmp
detun = qubFreq-driveFreq
Omega = np.sqrt((OmegaR**2) + (detun**2))

[11]:

qub = qg.QuantumSystem(operator=qg.Jz)
qub.dimension = 2
qub.frequency = qubFreq

# add the drive terms
secondTerm = qub.createTerm(operator=qg.sigmax)
secondTerm.frequency = driveFreq

qub.initialState = 1

qub.simTotalTime = 2*np.pi
qub.simStepSize = 0.01

# create the operators for which we compute the expectation values
sigmaX = qg.sigmax()

# write a compute function that takes two arguments: (i) a quantum-system (qsys) and (ii) a state
# compute whatever we want and store in .resultsDict
def compute(qsys, state):
    qsys.resultsDict['sigmax expectation'].append(qg.expectation(sigmaX, state))

# set the compute attribute of our qubit to compute function
qub.compute = compute

[12]:

def secondTermTime(st, ti):
    st.frequency = couplingStrength*driveAmp*np.cos(2*np.pi*driveFreq*ti + drivePhase)

secondTerm.timeDependency = secondTermTime

[13]:

states = qub.runSimulation()

[14]:

qub._freeEvol.numberOfExponentiations, len(qub.simulation.timeList)

[14]:

(1258, 630)

[15]:

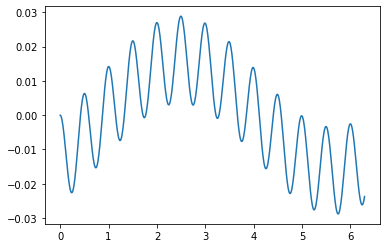
plt.plot(qub.simulation.timeList, qub.resultsDict['sigmax expectation'])

[15]:

[<matplotlib.lines.Line2D at 0x20f72eba5b0>]
../../../_images/classes_Tutorials_1_Qubit_14_Qubit_timeDependentTerm_7_1.png 
[ ]:

previous

13 - Multi-parameter sweep (simultaneously)

next

15 - Time dependent Hamiltonian 2